| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 科技知识 -> 世界上有哪些代码量很少,但很牛逼很经典的算法或项目案例? -> 正文阅读 |
|
|
[科技知识]世界上有哪些代码量很少,但很牛逼很经典的算法或项目案例? |
| [收藏本文] 【下载本文】 |
|
是不是代码越少越好?有什么典型例子吗?请教各位技术大神。 |
|
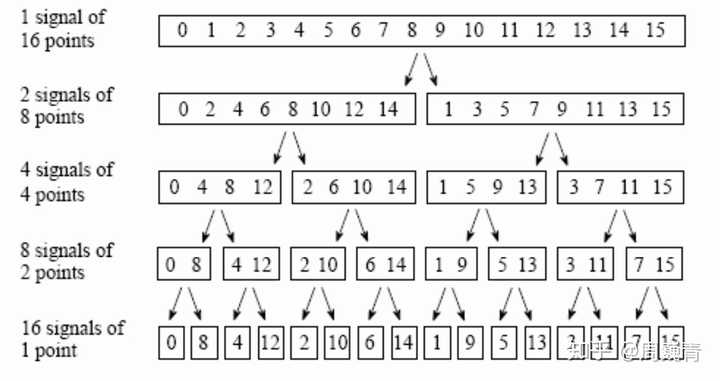
快速傅里叶变换(FFT),核心算法用递归法几十行搞定。 计算机应用最为重要的算法之一,广泛应用于各种各样的工业和科学实践中。第一次看到递归算出快速傅里叶的时候,惊了很久。后来经过数学家的很多努力,有了新算法将复杂度从N^2,降到N*log(N),觉得可以称之为人类智慧的精华了。 有空可以贴下源代码。 2020.1.15 这几天忙着科研,大家别急,今天一定抽空把算法和源代码贴出来。 第一次更新(1.15): 众所周知,数学中有一个傅里叶变换,是将函数在实空间的定义域变换到倒空间的定义域上,这个变换非常重要,因为一些实空间不易发现的信息,在倒空间中会表现的非常明显,所以傅里叶变换是很多信号、物理的分析基础。它的形式如下: H(f)=\int_{-\infty}^{\infty}h(t)e^{-2\pi ift}dt 以及其逆变换: h(t)=\int_{-\infty}^{\infty}H(f)e^{2\pi ift}df 但是如果在计算机想要编程实现傅里叶变换就要不可避免地面临两个近似:第一,现实中我们无法将积分的上下界延伸到无穷,所以这里一定是一个有界积分;第二,无论什么连续的公式,只要是想要被计算机实现,就必须进行离散化,所以这里的连续积分( \int )就近似为离散求和( \sum )。而基于这两种朴素近似下的,就是所谓的“离散傅里叶变换”(Discrete Fourier Transform,简称DFT),它的形式也很直观: H(f)=\int_{-\infty}^{\infty}h(t)e^{-2\pi ift}dt\approx\sum_{k=0}^{N-1}h_{k}e^{-2\pi if_{n}t_{k}}\Delta 看到这里,其实你如果利用DFT简单地编程,其实已经可以实现傅里叶变换了。但是我们为什么不用这个算法呢?是因为复杂度。 复杂度是算法中的一个概念,简单来说就是复杂度越高,那么这个算法计算大体系就越困难,那有多困难呢?我举个例子,现在算法基础库中对于矩阵的对角化应该是最基础和重要的了,矩阵的对角化的计算复杂度是 O(N^{3}) ,就是说对角化的时间就随着矩阵维数的三次方增加,这是十分恐怖的增长。目前市面的通用的对角化库,比如 lapcak,对角化的极限维数一般也就在 10000, 这个量级。那DFT的复杂度是多少呢?你可以从公式上看到,如果你现在要对一个包含N个数的数组进行DFT,那你每算其中一个变换后的数,都要进行N次的运算,那这个算法的复杂度也就是 O(N2)" role="presentation">O(N2)O(N^{2}) ,也就是说,用DFT最多也就只能处理大概一个拥有大概 106∼ 107" role="presentation">106~ 10710^{6}\sim~10^{7} 个数的数组。但是在生产科研实践中,这实在不是一个大的上限,所以这个复杂度的硬伤一直制约着DFT的发展,而这就是属于当时制约整个人类文明进步的“卡脖子”的难题,如果FFT没有出现,那我们的世界现在绝对不是现在这个样子。 时间来到1965年,James Cooley 和 John Tukey 发现了一种算法,这种的算法的复杂度降低为了 N×log2(N)" role="presentation">N×log2(N)N \times log_{2}(N) ,而这种算法就称之为“快速傅里叶变换”(Fast Fourier transform, 简称FFT)。但其实,就这个问题,Danielson 和 Lanczos 在1942年就已经开始了相关的讨论。他们发现任何一个DFT其实可以重新改写成两个DFT的和: Fk=∑j=0N−1e2πijk/Nfj=∑j=0N/2−1e2πik(2j)/Nf2j+∑j=0N/2−1e2πik(2j+1)/Nf2j+1=∑j=0N/2−1e2πikj/(N/2)f2j+Wk∑j=0N/2−1e2πikj/(N/2)f2j+1=Fke+WkFko" role="presentation">Fk=∑j=0N?1e2πijk/Nfj=∑j=0N/2?1e2πik(2j)/Nf2j+∑j=0N/2?1e2πik(2j+1)/Nf2j+1=∑j=0N/2?1e2πikj/(N/2)f2j+Wk∑j=0N/2?1e2πikj/(N/2)f2j+1=Fke+WkFko\begin{split} F_{k}&=\sum_{j=0}^{N-1}e^{2\pi ijk/N}f_{j}\\ &=\sum_{j=0}^{N/2-1}e^{2\pi ik(2j)/N}f_{2j}+\sum_{j=0}^{N/2-1}e^{2\pi ik(2j+1)/N}f_{2j+1}\\ &=\sum_{j=0}^{N/2-1}e^{2\pi ikj/(N/2)}f_{2j}+W^{k}\sum_{j=0}^{N/2-1}e^{2\pi ikj/(N/2)}f_{2j+1}\\ &=F^{e}_{k}+W^{k}F^{o}_{k} \end{split} 数学家进一步发现这一分为二的DFT组,一个是原来是偶数项(even,第0,2,4,6...项)组成的,而另一个是由原来的奇数项(odd)组成的。如果你只是看到这一步,你已经发现了一个大事情,就是原来用这个公式来算的话,求一个傅里叶变换不再需要进行N次相乘,而只需要odd组的N/2次运算,even组的直接不用做任何运算直接拉下来就好了。那这样计算量不就减少一半了吗?但是其实事情并没有那么简单,我们刚才证明了任何一个DFT组都能被一分为二,而且计算量减半。但是我们现在一分为二得到的even组和odd组,他们不又是DFT组吗?我们可以继续之前的操作,将他们分别再次分为两个数组的求和! |
|
|
Fig.1 DFT的细分过程 一分为二,二分为四,四分为八,一直分到每个数组只剩一个数字为止!而且每进行一次操作,就能使得其中一半的计算量被减少。这样我们就把计算量从 O(N2)" role="presentation">O(N2)O(N^{2}) 降到了 N×log2(N)" role="presentation">N×log2(N)N \times log_{2}(N) 。你可能现在对这个算法的突破性还没有概念,我现在来给你构建下概念, N=1024,N/log2(N)∼102N=8192,N/log2(N)∼630N=32768,N/log2(N)∼2185N=106,N/log2(N)∼50171" role="presentation">N=1024,N/log2(N)~102N=8192,N/log2(N)~630N=32768,N/log2(N)~2185N=106,N/log2(N)~50171N=1024, N/log_{2}(N)\sim102 \\ N=8192, N/log_{2}(N)\sim630 \\ N=32768, N/log_{2}(N)\sim2185 \\ N=10^{6}, N/log_{2}(N)\sim50171 随着N的增加,FFT算法对于DFT的优势会不断显现,一开始1024个数,FFT比DFT快100倍;32768个数,就快了2000多倍,到了我们之前提到的极限1百万个数,快了近5万倍!FFT将我们的计算分析能力成万倍的提升。提一句,现在FFT最稳定最快的库是FFTW,这个W是“in West”,就是说“西方的FFT”。我当时刚看懂FFT时,不服气,一心想写个东方版,FFTE(FFT in East),后来和我自己的程序和FFTW性能一比,我人都傻了,果然好的FFT程序还是超级难写的。 这个算法关键的关键就是将DFT组不断奇偶细分,细分到最后时,如何确定每个数组前面的相位系数。我希望今天可以在第二次更新中把如何确定细分后的序列,以及蝶形算法更完。 |
|
|
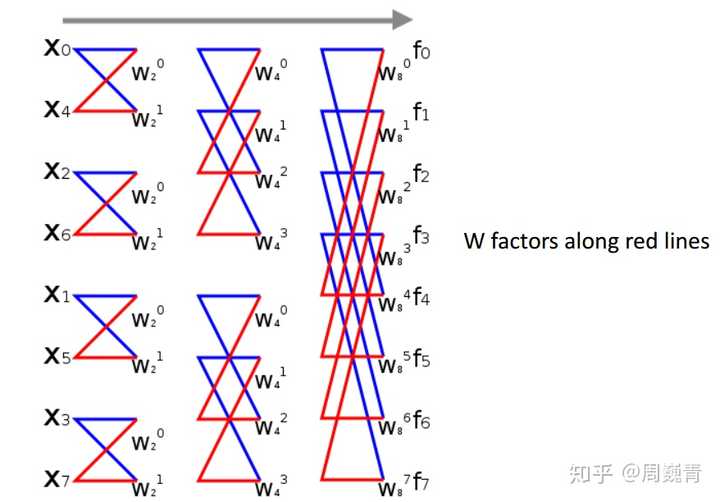
Fig.2 蝶形算法 我先把我当时研一第一次接触到FFT编写的Fortran源码贴出来吧。短短几十行,如果你能花几天的时间理解这个递归程序,那么这将是2020年获得的第一个受益终身的知识。 2023.2.19 感谢评论区的建议,将 o" role="presentation">oo 改为 O" role="presentation">OO 。 |
|
居然没人说这个在GitHub上拿到34k星的项目?难道知乎上的程序员都只逛百度,不逛GitHub? 这个项目堪称传奇,在GitHub上被无数人称赞为新手必学项目,却偏偏又可以无需任何修改,就在任何平台、版本的IDE上运用,真正的0成本接入,堪称有史以来最伟大的工程,没有之一! 为了尊重原作者,请大家去项目中查看,绝对是计算机历史上的一座丰碑。 我上面的话,可不是我自己评价的,都是网友们的留言: |

|
|
|
|
|
|
|
|
|
|
|
|
|
|
这也是我见过第一款,被中外老哥用花式语言夸奖的项目,比如Book思议(不可思议),甚至很多人用:道可道,非常道、无极、凝视深渊这里很有哲理的话来夸奖。 整个GitHub,甚至往大了说,全网你都找不到第二个这样的项目了! 项目名称:nocode 项目地址:https://github.com/kelseyhightower/nocode 等你心平气和,仔细看完项目就会明白,这个项目贯彻了git这个词的本意。 而且程序员其实有三重境界: 1.眼中有码,敲键盘如有神助。 2.心中有码,无码也有码,对于代码的理解近乎于道。 3.心中无码,有码也无码,他就是道。 只有到达第三重境界才能迈过35岁这个坎 我看完这个项目之后的感想: 再给大家来个硬核项目:99行代码实现《冰雪奇缘》! 《冰雪奇缘》没有真人出演,预算却高达1.5亿美元,每一秒的镜头都是经费在燃烧。一般人想用电脑做出CG特效简直不可想象。 然而,最近一位来自中国的MIT博士,开发了物理模拟编程语言:Taichi 大大降低了成本。 计算机图形学知名学者、北大教授陈宝权给出很高的评价: |
|
这段代码用Python 3运行。运行前要根据操作系统和CUDA版本(如果有CUDA的话)安装taichi: 这99行代码虽然很短,其背后的故事却很长。 虽然语法看起来是Python,其计算部分却会被一整套编译系统接管,最后输出可执行的x86_64或者PTX instructions,能够在CPU/GPU上高效运行。 |

|
|
0 项目地址:https://github.com/yuanming-hu/difftaichi 延伸阅读: GitHub 上有什么「不能错过」,简单、易学的 Python 项目?2763 赞同 · 25 评论回答 |

|
|
如果你想了解更多有趣、有观点、有知识的内容,别忘记点击 @东来 关注我,一个有趣的人在默默的等着你! 我还写了不少“宝藏”内容, 可以来看看我19年的高赞内容,横跨编程、旅行、体育三大板块,好几个是单篇数百万阅读的硬核科普内容。 我19年创作的高赞内容,来看看吗?4222 浏览 · 89 关注收藏夹 |

|
|
|
|
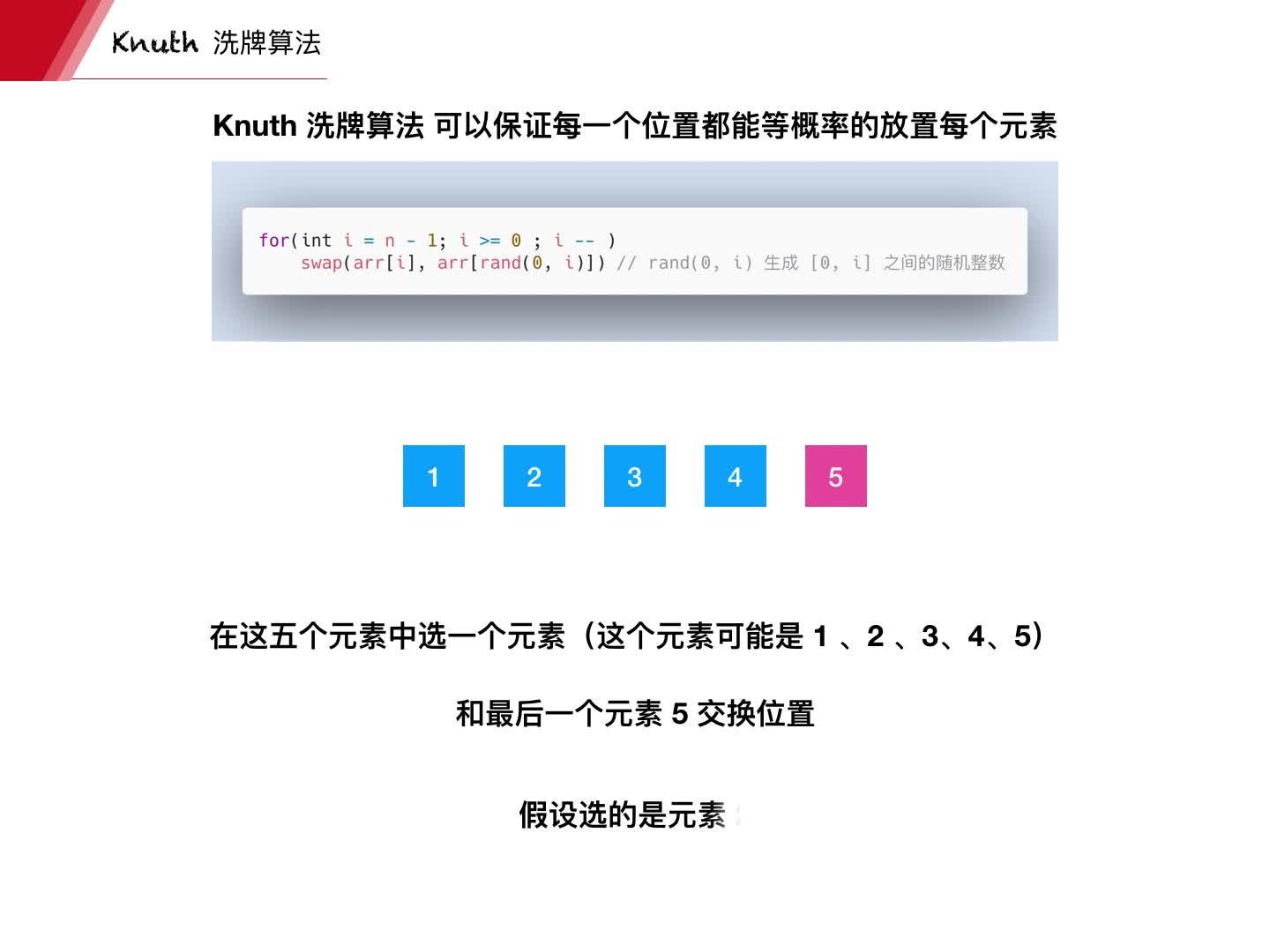
有的,比如 洗牌算法:这个算法真的很牛逼很经典,而且代码很少。 评论区好多大佬,膜拜ing。。 先来思考一个问题:有一个大小为 100 的数组,里面的元素是从 1 到 100 按顺序排列,怎样随机的从里面选择 1 个数? 最简单的方法是利用系统的方法 Math.random() * 100 ,这样就可以拿到一个 0 到 99 的随机数,然后去数组找对应的位置就即可。 接下来在思考一个问题: 有一个大小为100的数组,里面的元素是从 1 到 100 按顺序排列,怎样随机的从里面选择 50 个数? 注意数字不能重复! 注意数字不能重复! 注意数字不能重复! 如果根据上面的思路,你第一想法是:随机 50 次不就行了? 但是,这样做有个很明显的 bug :数字是会重复的。 修改一下? 弄一个数组,把每一次随机的数都放到数组里,下一次随机就看这个数组里面有没有这数,有的话就继续随机,直到这个数组里面有 50 个数字就停止。 这样是可以的! 但,还是有个小问题,考虑一下极端情况:有一个大小为100的数组,里面的元素是从 1 到 100 按顺序排列,怎样随机的从里面选择 99 个数。 如果按照上面的方法操作,越往后选择的数字跟前面已经挑选的数字重复的概率越高,这就会造成如果数组很大,选择的数字数目也很大的话,重复次数在量级上会很大。 这个时候就需要换一个思路,如果先将数组里面的元素打乱,那么按顺序选择前 50 个不就可以了? 是的! 但我们得注意什么叫乱? 一副扑克有 54 张牌,有 54! 种排列方式。所谓的打乱指的是,你所执行的操作,应该能够 等概率地生成 这 54! 种结果中的一种。 洗牌算法就能做到这一点。 洗牌算法 Fisher–Yates shuffle 算法由 Ronald Fisher 和 Frank Yates 于 1938 年提出,在 1964 年由 Richard Durstenfeld 改编为适用于电脑编程的版本。 这个算法很牛逼却很好理解,通俗的解释就是:将最后一个数和前面任意 n-1 个数中的一个数进行交换,然后倒数第二个数和前面任意 n-2 个数中的一个数进行交换。。。 |

|
|
小程序实现代码 在整个过程中,这个算法保证了每一个元素出现在每一个位置的概率是相等的。 这个算法真的很牛逼很经典,而且代码很少。 我做了一个视频进行辅助理解。 |
|
|
0 洗牌算法:) 为了避免知乎大佬觉得我吹逼,先贴一下自己的 GitHub 地址,目前 70,000 star,全球排名 51 名。 https://github.com/MisterBooo |
|
|
算法是一种技能,是可以通过科学合理的方式训练出来的能力。 在想刷题之前,得从心里认识到接受刷题很重要,才能坚持去刷题。 江湖有个传言:国内刷 LeetCode,最多够你吃 1 年老本;湾区刷 LeetCode ,够你吃 10 年老本了。 为什么湾区的刷题性价比这么高呢? 你想想,电面考 4 道题,一道题值 5 万!单位是 Dollar ! |

|
|
刷到就是赚到!! 想想是不是很刺激,有没有动力开始刷题了!可以提速刷题了! 就目前互联网的情况来说,无论是面国外大厂还是面国内大厂,如果想换工作都要去刷题,一面二面不丢你几道 Hard 题,都对不住你偷偷摸摸找个会议室假装开会实则面试的鸡贼。 同时,还得认识到一点,面试能力和你平时的工作能力其实差别挺大的。 有些人技术挺厉害的,但没有刷题,一面二面都过不了,而某些小镇刷题家,还真就靠刷题拿下了 Google、微软、脸书等大厂offer。 国内大厂也有这种趋势,比如字节,一大半都是面试题。 |
|
|
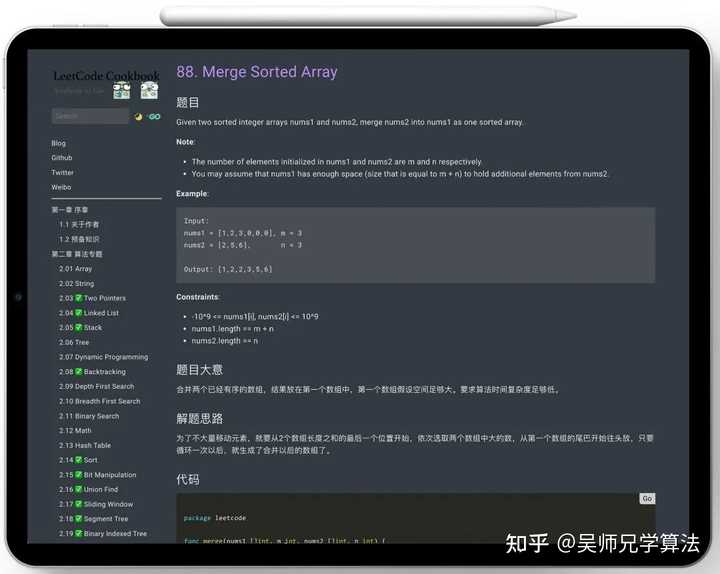
要不是他提前先看视频刷题,妥妥得凉凉。 所以,刷题很重要。 (PS:感谢大家耐心的阅读,算法是程序员的重中之重,必须攻克,大厂面试必考,顺便送一份阿里大佬刷Leetcode总结的算法笔记,如果你能吃透,那我相信80%的技术面试都会不在话下: BAT大佬写的Leetcode刷题笔记,看完秒杀80%的算法题! 这本书的目录,非常经典: |
|
|
刷题大概可以分为 4 个阶段。 1、纯小白,不知道怎么刷题,对很多概念都很陌生,各种数据结构和知识点几乎完全不懂,打开 LeetCode 第一题,满头问号。 有人相爱、有人夜里开车看海、有人 LeetCode 第一题都做不出来。 2、算法上基本已经入门,Easy 可以做出来,Medium 纠结半天也能有头绪,但基础不牢,比如字符转字符串还得 Google 一下。 3、刷了几百道题后,总结了自己的解题模板,参加周赛有时候甚至可以全部完成。 4、开始以 beat 100% 作为 AC 的目标了。 就目前的算法面试大环境来说,能达到第二阶段,中小公司可以应付过去了,到达第三阶段,字节、腾讯算法面试环节妥妥没问题了。 怎么样到达第三阶段? 给一下我的一些小建议吧。 1、如果目标是国内大厂,那么一定要刷足够的题,不需要把 LeetCode 上 2500 道算法题都刷完,但至少刷 200 道算法高频题,这些高频题我都写了题解同时也录制了视频, 在这个链接总结了:https://www.algomooc.com/1659.html 2、面试前一周以看题为主,因为刷题也刷不了几题,多看看自己总结或者别人总结的模板,比如回溯算法模板,掌握后,几十道回溯题都不在话下。 一些模板: 回溯,不难!?mp.weixin.qq.com/s/2CLyNJtTnVQeEsy4fPC3Eg |

|
|
3、刷题过程需要注意难度要循序渐进,算法训练是一个系统工程,需要循序渐进,太过于急功近利,反而容易因做不出难题而产生挫败感,带来反效果。 如果你本身有基础,熟练度高,那你刷简单的 LeetCode 应该是几分钟一题,几分钟一题的,花不了你多少时间。 如果你刷简单都花费很长时间,说明熟练度不够,就更应该从简单开始,然后过度到中等,再过度到困难。 并且,目前国内大厂的算法考察,基本不会超过 LeetCode 中等难度,上限难度基本都是 LeetCode 中等题里面的中等难度,所以不要太去纠结难题怪题偏题。 把高频题掌握就行了:https://www.algomooc.com/1659.html 再退一步,如果你觉得 LeetCode 的题目太难,可以先从《剑指 Offer》上的算法题开始学起。 为了帮助大家更好的入门学习算法,经过半年的积累,我给大家卷了《剑指 Offer》系列的三十道题目,结合动画的形式录制了视频,相信能帮助你更好的刷题。 |
|
|
领取地址: 当《剑指 Offer》上的题都变成了动画?mp.weixin.qq.com/s/sk2kPb1rogmg9SmOfQ1nLw |

|
|
4、按算法分类来选题,比如一个时间段,只刷链表题,刷得差不多的时候,接下来再刷二叉树的题。 这样做有几个很明显的好处。 一、持续地刷同个类型的题目,可以不断地巩固和加深理解,可以总结出自己的思考路径或者解题模板。 比如链表题目,就会去思考虚拟头节点、双指针、快慢指针。 二、可以更全面地接触这个数据结构,算法的各个变种,这会促使你对这个数据结构,算法的理解更加全面和深刻,学习的效率会更高。 我一直认为读书是世界上性价比最高的成长方式,书很便宜但分量很重,是让我们摆脱平庸走向卓越的方式之一。 对于计算机专业的学生而言,读计算机经典书籍不光能让你快速提升知识和能力,更会让你在校招之际如虎添翼。 书籍下载:计算机必看经典书籍(含下载方式) |

|
|
最后,再给大家送上点干货! 下面这是一个高赞回答合集,建议大家点赞&收藏,Mark住别丢了,大学期间绝对用得上。 1、怎么学好数据结构,看下面这个回答,已经获得了 21000+ 的赞和 50000+的收藏。 2、如何系统地学习算法,看下面这个回答,已经获得了 11000+ 的赞和 26000+的收藏。 3、新手该如何使用 GitHub,看下面这个回答,如果在大学期间就知道使用 GitHub ,那么能力远超同龄人。 4、想成为一名优秀的程序员,那么这些程序员平时都喜欢逛的论坛怎么说你也得收藏一些吧。 5、无论别人怎么说,我都是坚定不移的选择计算机专业。 6、如何系统地学习 C++ ,这个回答能帮你找到路线。 7、想要准备 Java 面试,那么这些面试题必须掌握。 赶紧点赞和收藏吧~ |

|
|
godweiyang 42 次咨询 5.0 字节跳动 员工 32999 次赞同 去咨询 我来提一个简洁的算法,用来求解:约瑟夫环问题。 有 n 个人围成一个圈,每 q 个人踢掉一个人,问最后留下来的人是几号? 是不是很熟悉?当初你们刚学的时候怎么做的?是不是用链表?是不是写得痛不欲生,还超时了?哦不是那算了。 如果用链表暴力求解的话,时间复杂度是 O(qn) ,但是用我下面的方法,可以加速到 O(\log{n}) 。 下面我讲一个具体数学课上讲到的简洁解法: 假设初始编号为 1,2,\ldots,n ,现在考虑一种新的编号方式。 第一个人不会被踢掉,那么他的编号从 n 开始往后加 1 ,变成 n+1 ,然后第二个人编号变为 n+2 ,直到第 q 个人,他被踢掉了。 然后第 q+1 个人编号继续加 1 ,变成了 n+q ,依次下去。 考虑当前踢到的人编号为 kq ,那么此时已经踢掉了 k 个人,所以接下去的人新的编号为 n + k(q - 1) + 1 \ldots 。 所以编号为 kq+d 的人编号变成了 n + k(q - 1) + d ,其中 qn ,问题是怎么根据这个编号推出他原来的编号? 以 n=10,q=3 为例,下图就是每个人新的编号: |

|
|
令 N = n + k(q - 1) + d ,那么他上一次的编号是 kq + d = kq + N - n - k(q - 1) = k + N - n 因为 k = \frac{ {N - n - d}}{ {q - 1}} = \left\lfloor {\frac{ {N - n - 1}}{ {q - 1}}} \right\rfloor 所以上一次编号可以写为 \left\lfloor {\frac{ {N - n - 1}}{ {q - 1}}} \right\rfloor + N - n 因此最后存活的人编号可以用如下的算法计算: 其中 k = \left\lfloor {\frac{ {N - n - 1}}{ {q - 1}}} \right\rfloor 。 如果我们用 D = qn + 1 - N 替代 N ,将会进一步简化算法: \begin{array}{l}D = qn + 1 - N\\ = qn + 1 - \left( {\left\lfloor {\frac{ {(qn + 1 - D) - n - 1}}{ {q - 1}}} \right\rfloor + qn + 1 - D - n} \right)\\ = n + D - \left\lfloor {\frac{ {(q - 1)n - D}}{ {q - 1}}} \right\rfloor \\ = D - \left\lfloor {\frac{ { - D}}{ {q - 1}}} \right\rfloor \\ = D + \left\lceil {\frac{D}{ {q - 1}}} \right\rceil \\ = \left\lceil {\frac{q}{ {q - 1}}D} \right\rceil \end{array} 算法伪代码如下: 其中 k = \left\lceil {\frac{q}{ {q - 1}}D} \right\rceil 。 最后用这个算法来求解一道经典约瑟夫环题目,题目链接: 注意到这题 n 的范围高达 10^{12} ,不管用 O(qn) 的暴力还是 O(n) 的递归都会原地爆炸boom boom boom~ 这时候就得动用上面的方法了。 C++代码如下: 详细的背景知识我写在了专栏文章里: 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
Tomohiko Sakamoto 算法,来确定当前日期是星期几 代码量很少,最少的实现方式只有一行,最多也不过四行。 但是相当经典,当然了,并不太容易理解。 Tomohiko Sakamoto 算法,最初实现代码: 同时,Tomohiko Sakamoto 还发布了另外一个更简洁的一行版本: 代码看着就很漂亮,分析一下会发现确实很漂亮。 |

|
|
|

|
|
|

|
|
|
|
|
| [收藏本文] 【下载本文】 |
| 科技知识 最新文章 |
| 百度为什么越来越垃圾了? |
| 百度为什么越来越垃圾了? |
| 为什么程序员总是发现不了自己的Bug? |
| 出现在抖音评论区里边的算命真不真? |
| 你认为 C++ 最不应该存在的特性是什么? |
| 为什么 Windows 的兼容性这么强大,到底用了 |
| 如何看待Nvidia禁止使用翻译工具将cuda运行 |
| 为何苹果搞了十年的汽车还是难产,小米很快 |
| 该不该和AI说谢谢? |
| 为什么突破性的技术总是最先发生在西方? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |